Editor's note: We are all like children in front of machine learning. When just learning the backpropagation algorithm, many people will not be satisfied with the most basic perceptron and try to build a deeper neural network with more layers. They admire their own realization, just like a child on the beach proudly looking at their own castle made of sand. But just like the mere appearance of the castle, the performance of these neural networks is often unsatisfactory. They may fall into endless training, and perhaps the accuracy rate will never be improved. At this time, some people will start to wonder: Isn't neural network the most advanced technology?

Everyone has had similar doubts--
The training process of neural network includes forward propagation and back propagation. If the prediction result obtained by forward propagation does not match the actual result, it means that the network is not well trained, and back propagation must be used to readjust each weight. This involves various common optimization algorithms. Taking gradient descent as an example, the idea is to use the negative direction of the current gradient as the search direction, and adjust the weight to make the objective function approach the local minimum, that is, let the cost function/ The loss function is getting smaller and smaller.
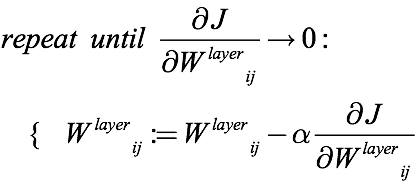
As mentioned in the above formula, the gradient descent algorithm uses the original weight to subtract the gradient multiplied by the scalar α (between 0 and 1) to update the weight, and "repeat" this process until convergence. But in actual operation, the number of iterations of this "repetition" is an artificially selected hyperparameter, which means that it may be too small, and the final convergence effect is not good; it may also be too large, and the network is trained "endlessly" Up". Therefore, there is an embarrassing situation between the training time and the training effect.
So how does this hyperparameter affect convergence? Just like different people have different descending speeds, gradient descent has a descending step length. The shorter the iteration time, the larger the step length. Although the convergence speed is fast, it is easy to fail to accurately converge to the final optimal solution; on the contrary, If the iteration time is too long and the step size is smaller, it is possible that the weight of the network will not change much during a long period of convergence, and it is relatively large, and the small step size is close to the minimum within the specified number of iterations. Harder.

Small steps converge like a "snail"
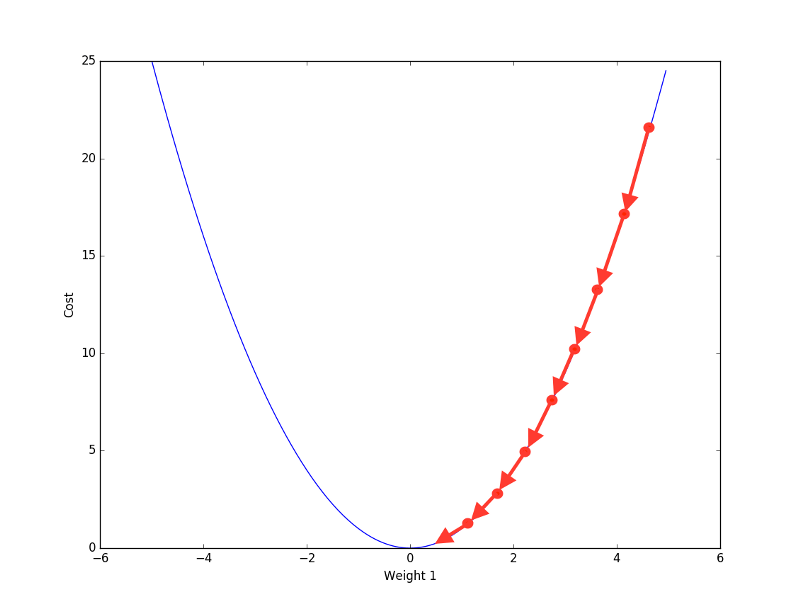
Large step size convergence is more efficient
This is not the only problem. When the gradient value is too small, it is easy to be rounded to 0, that is, underflow. At this time, some operations on this number will cause problems.
Seeing this, we seem to have got the fact: small gradient = bad. Although this conclusion may seem arbitrary, in many cases, it is not alarmist, because the disappearance of the gradient in this article is caused by small gradients.
Let us recall the sigmoid function, which is an activation function often encountered in classification problems:
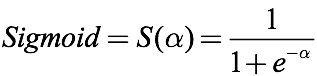
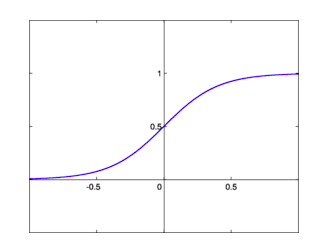
As shown in the figure above, the role of sigmoid is indeed obvious to all. It can limit any input threshold between 0 and 1, which is very suitable for probability prediction and classification prediction. But in the past few years, sigmoid and tanh have not become popular. When it comes to activation functions, the first thing that comes to mind is ReLU. Why?
Because sigmoid is almost synonymous with vanishing gradient, we first seek its derivative:
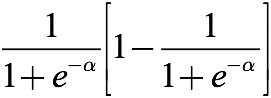
This seems to be a very ordinary s(1-s) formula, which seems to be no problem. Let's draw its image:
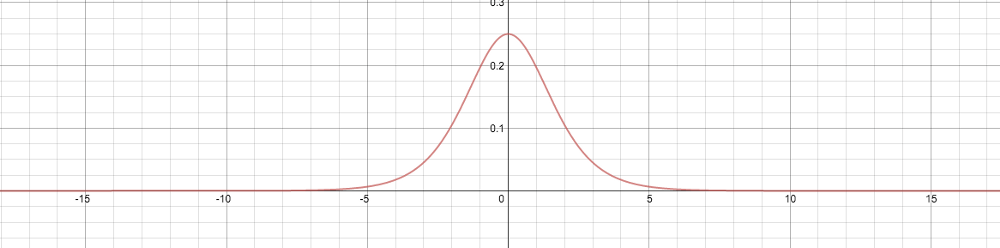
Take a closer look, is it okay? It can be found that the maximum value in the above figure is only 1/4, and the minimum value is infinitely close to 0. In other words, the threshold of this derivative is (0, 1/4]. Remember this value, we will use it later.
Now let's go back and continue to discuss the back propagation algorithm of neural networks to see what effect the gradient will have on them.

This is the simplest neural network. In addition to the input neurons, the act() of other neurons comes from the neurons in the previous layer: first multiply the weight by act(), and then feed it into the next layer through the activation function. The information from the upper layer becomes a brand new act(). The final J summarizes all the error terms (error) in the feedforward process, and outputs the overall error of the network. After that, we perform backpropagation and modify the parameters through gradient descent to minimize the output of J.
Here is the derivative of the first weight w1:

We can use the derivative of the weight to perform gradient descent, and then iterate to find the global optimal point, but before that, this derived multiplication operation is worth paying attention to:
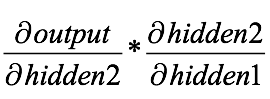
Since the output of the previous layer multiplied by the activation function is the input of the next layer, the above formula actually includes the derivative of sigmoid. If all the information is expressed intact, the expression returning from the output to the second hidden layer should be:
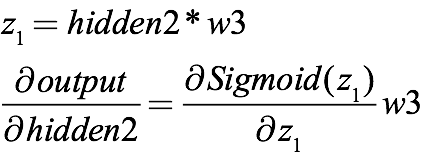
Similarly, from the second hidden layer to the first hidden layer is:
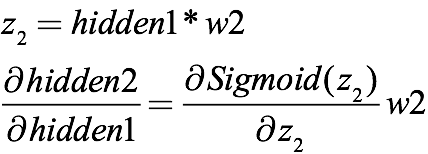
They all contain the sigmoid function, which together are:
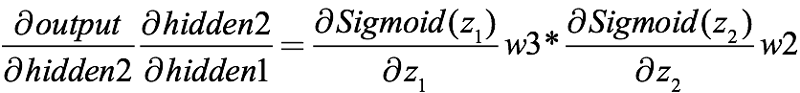
We have taken the derivative of sigmoid before, and calculated its threshold is (0, 1/4]. Combined with the above formula, two decimals between 0 and 1 are multiplied, and the product is less than any multiplier. In the typical In the neural network of, the general method of weight initialization is that the selection of weights should obey the normal distribution with mean=0 and variance=1, so the threshold of these initial weights is [-1, 1].
The next thing is clear:
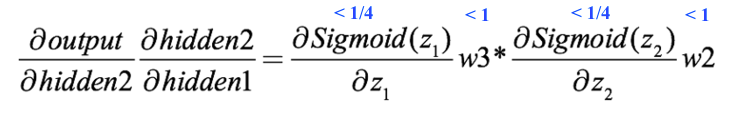
Even without the conventional weight initialization method, w2 and w3 are greater than 1, but they are still a drop in the bucket for the multiplication of the two sigmoid derivatives, and the gradient becomes too small. In actual operation, the random weight is likely to be less than 1, so at that time it was actually helping the gangsters.
There are only 2 hidden layers. Just imagine if this is an industrial-grade deep neural network, then when it is performing backpropagation, how small the gradient will become, it is reasonable to make it disappear suddenly. . On the other hand, if we control the absolute value of the derivative of the activation function to be greater than 1, then this multiplication operation is also very scary, and the result will be infinite, which is what we often call "gradient explosion".
Now, let’s look at a typical ANN:
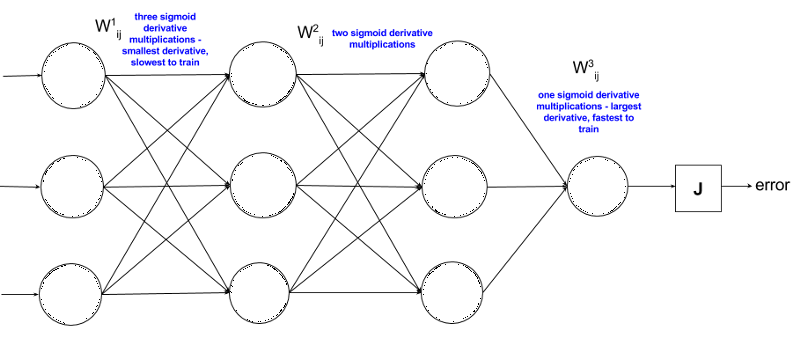
The weight of the first term is the farthest from the error term J, so its expression is the longest after derivation, it also contains more sigmoid functions, and the calculation result is smaller. Therefore, the first layer of the neural network is often the one with the longest training time. It is also the basis of all the following layers. If this layer is not accurate enough, it will have a chain reaction and directly reduce the performance of the entire network.
This is also the reason why neural networks, especially deep neural networks, were not accepted by the industry at first. The correct training of the first few layers is the foundation of the entire network, but the defects of the activation function and the insufficient computing power of the hardware equipment made it impossible for the researchers at that time to lay a good foundation.
Seeing this, we should all have understood the shortcomings of the sigmoid function. Although its alternative tanh function was once famous, considering tanh(x)=2sigmoid(2x)-1, it must have the same problem. . So, what's so good about ReLU that everyone is using now?
First, ReLU is a piecewise function:
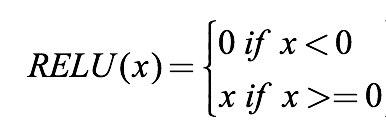
It also has another way of writing:
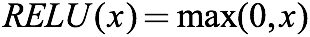
When the input is less than 0, the function outputs 0; when the input is greater than zero, the function outputs x.
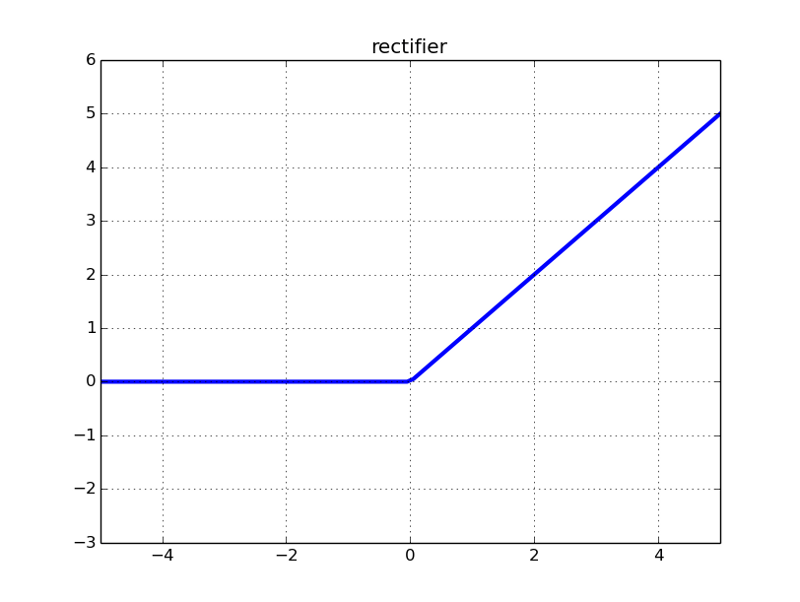
We calculate its derivative to compare sigmoid:
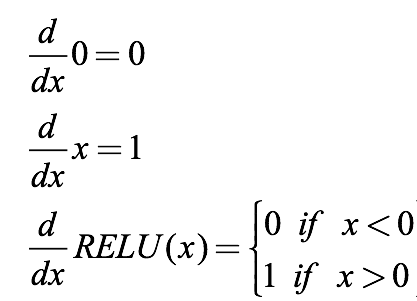
Then there is its image, pay attention to one point, it is not differentiable at 0, so when x=0, there should be two hollow circles on the y axis in the figure.
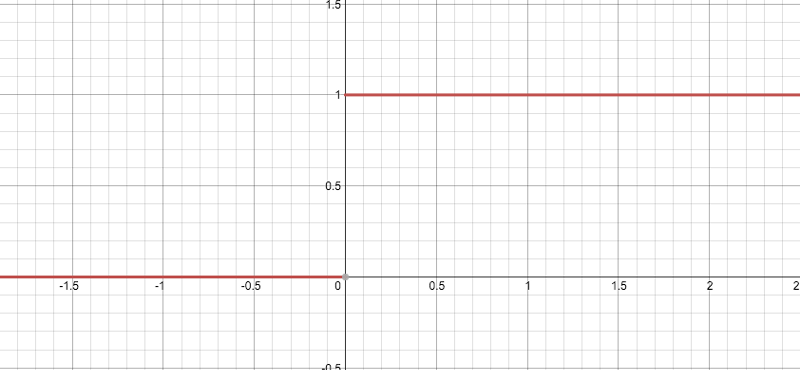
It can be found that the threshold of the derivative is finally no longer (0, 1). It seems to prevent the gradient from disappearing, but it seems something is wrong? When we input a negative value into the ReLU function, the gradient is 0, and the neuron is "necrotic" at this time. In other words, if there are negative weights, some neurons may never be activated, causing the corresponding parameters to never be updated. In a sense, ReLU still has the problem of partial gradient disappearance.
So, how do we choose? No hurry, there is also an activation function-Leakly ReLU.
Since the "gradient disappearance" of ReLU is derived from its threshold value of 0, we can reset it to a specific decimal between 0 and 1. After that, when the input is negative, it still has a very small gradient, which provides an opportunity for the network to continue learning.
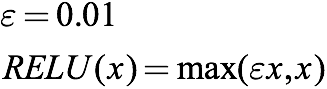
In the above formula, ε=0.01, but its most common range is 0.2-0.3. Because the slope is small, after inputting a negative weight, it is a very gentle line on the image:
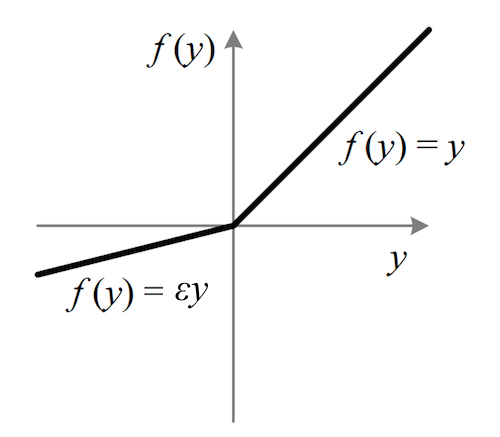
Here we want to make a statement: Although Leakly ReLU can solve the neuron necrosis problem of ReLU, its performance is not necessarily better than ReLU. For example, if the constant ε is too small, it is likely to cause the new gradient to disappear. On the other hand, these two activation functions have a common disadvantage, that is, they are not bounded like tanh and sigmoid. If it is in a deep neural network like RNN, even if the derivative of ReLU is 0 or 1, it is very small. But besides it, we still have so many weights. Multiple multiplications will result in very large output values, and then the gradient will explode.
So in general, ReLU does not cure the problem of gradient disappearance, it only relieves the contradiction to a certain extent and creates another new problem. This is why these activation functions can still coexist so far-CNN uses ReLU more commonly, while RNN mostly uses tanh. In the context of "metaphysics", this is probably the first trade off that novices come across after getting started with machine learning.
Tpu Screen Protector,TPU Film Sheets,Phone Use Tpu Screen Protector,Tpu Phone Screen Protector
Guangdong magic Electronic Limited , https://www.magicmax.cc