Hello, everyone, but also to the time of daily learning, and today we talk about digital signal processing DFT, DTFT and DFS relationship, let's compare through several plans to discuss Oh.
After learning a lot of digital signal processing, many students were confused by several nouns, such as DFT, DTFT, DFS, FFT, FT, FS, etc. FT and FS belong to the course of signal and system courses, and they are for continuous time signals. Processing, there is no more discussion, only explain the relationship between the first four.
First of all, I'm not a digital signal processing expert, so I'm only talking from the learner's point of view to explain the problem in the most easily understandable nature, without involving any formula operation.
Having studied convolutions, we all know sometimes the domain convolution theorem and the frequency domain convolution theorem. Here we only need to remember two points: 1. The multiplication in one domain is equal to the convolution in the other domain; 2. The pulse function The convolution produces a mirror image of the waveform at each pulse position. (In any signal and system textbook, these two properties have a detailed formula to prove)
In the following, these two properties are used to illustrate the links between DFT, DTFT, DFS, and FFT:
Look at the picture first: 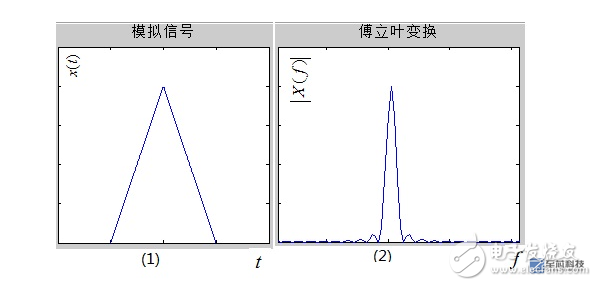

First of all, figure (1) and figure (2), for an analog signal, as shown in Figure (1), to analyze its frequency components must be transformed to the frequency domain, which is through the Fourier transform FT (Fourier Transform) The resulting spectrum of the analog signal is shown in (2). Note 1: Both the time domain and the frequency domain are continuous!
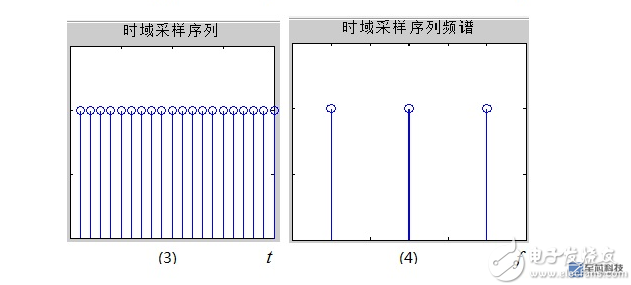
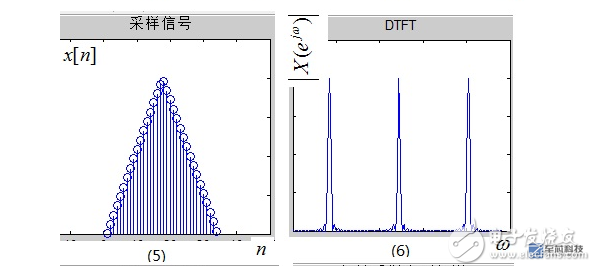
However, the computer can only process digital signals. First, the original analog signal needs to be discretized in the time domain, that is, it is sampled in the time domain. The sampling pulse sequence is shown in (3), and the spectrum of the sampling sequence is shown in (4). ), it can be seen that its spectrum is also a series of pulses. The so-called time-domain sampling is to multiply the signal in the time domain, (1) × (3) can be obtained after the discrete-time signal x [n], as shown in Figure (5); by the preceding property 1, the time domain The multiplication is equivalent to the convolution of the frequency domain. Then, the image (2) and the image (4) are convolved. According to the property 2 above, the image appears at each pulse point, and the image (6) is obtained. The DTFT (Discrete time Fourier Transform) of the discrete-time signal x[n] shown in FIG. 5 is a discrete-time Fourier transform. Here, four words of “discrete time†are emphasized. Note 2: The time domain is discrete and the frequency domain is still continuous.
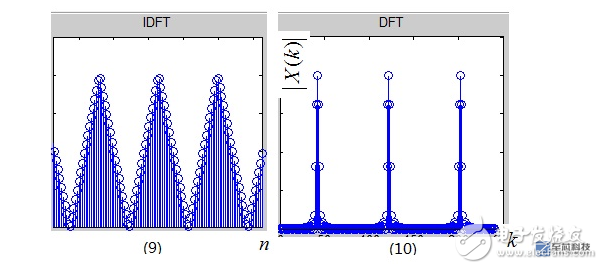
After the above two steps, the signal we get is still not processed by the computer because the frequency domain is continuous and periodic. We naturally think that since the time domain can be sampled, why can't the frequency domain sample it? Isn't this time domain and frequency domain discretized? It is true that the frequency domain is sampled next. The spectrum of the frequency domain sampling signal is shown in (8), and its time domain waveform is shown in (7). Now we perform frequency-domain sampling, ie, frequency-domain multiplication. Figure (6) × Figure (8) yields Figure (10). Then according to property 1, this time is the frequency-domain multiplication, the time-domain convolution, Figure ( 5) Convolved with graph (7) to obtain (9). As expected, the mirror image appears periodically at each pulse point. We take the main value interval of the (10) periodic sequence and denote it as X(k), which is the DFT (Discrete Fourier Transform) of the sequence x[n], that is, the discrete Fourier transform. It can be seen that the DFT is only for the convenience of computer processing, sampling the DTFT in the frequency domain and intercepting the main value. Someone may wonder, IDFT the graph (10) and return to the time domain (9), which is different from the x[n] shown in the original discrete signal graph (5). It is the periodicity of x[n]. Continuation! That's right, so you're looking for an IDFT definition. Isn't that limiting the n value range? The meaning of this restriction is that the main value interval of the periodic extension sequence can be used to restore x[n]!
FFT? The FFT is proposed solely for the fast calculation of DFT. Its essence is DFT! Our commonly used signal processing software MATLAB or DSP software package contains algorithms that are FFT instead of DFT.
DFS is proposed for the time domain periodic signal. If DFS is applied to the periodic extension signal shown in (9), figure (10) will be obtained. As long as the main value interval is intercepted, it is a complete one-to-one correspondence with DFT. The exact relationship. This can be easily seen by comparing the definition of DFS and DFT. Therefore, the essence of DFS and DFT is the same, but the method described is different.
Do not know that after the above explanation, do you understand the relationship between various T? If you are not an algorithm designer, you only need to know how to use FFT to analyze the spectrum. The blogger will update an article in the near future to specifically explain how to use FFT to analyze the spectrum of simple signals.
In fact, personally think that tangled up so much is to break the boundaries between the real world of simulation and the digital world of computers!
Talk to you today, everyone, come on.
We are dedicated charging solution Manufacturer since 2005.
Supply various Power Station including Portable Power Stations, Solar Power Generators, Smallest Generator etc.
Manufacturing high quality products for customers according to international standards, such as CE ROHS FCC REACH UL SGS BQB etc.
To constantly offer clients more innovative products and better services is our consistent pursuit.
portable power stations for camping, solar pow er stations, jackery portable power station
TOPNOTCH INTERNATIONAL GROUP LIMITED , https://www.micbluetooth.com